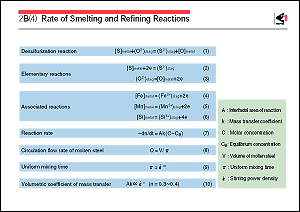
The various smelting and refining reactions involved in the iron and steelmaking processes generally proceed at high temperatures, so there are few cases where the chemical reaction rate controls the overall reaction rate. For example, the desulfurization of molten steel by slag shown in Eq. 1 is composed of the elementary reactions given by Eqs. 2 and 3 and the associated reactions given by Eqs. 4, 5 and 6. It is known that these elementary and associated reactions are rate-controlled by mass transfer of the reactants in less than 1 second from the start of the reactions. As with decarburization, desulfurization and dephosphorization, when the overall reaction is rate-controlled by the reactant's mass transfer to the reaction interface, the change in the reactant's mole number "n" after time "t", i.e., the reaction rate "-dn/dt", can be expressed by Eq.7 as a function of area "A" of the reaction interface, mass transfer rate constant "k", the reactant's molar concentration "C", and equilibrium concentration "Ce". To increase the rate "-dn/dt" of the overall reaction (the overall mass transfer rate), it is necessary to make "Ak" (the volumetric coefficient of mass transfer) large and "Ce" small. The conditions for making "Ce" small are determined by a thermodynamic consideration. For any reaction of a gas/metal system or a slag/metal system, "Ak" can be made very large by blowing gas or slag into the metal bath or by enhancing the stirred flow and intermixing the slag and metal. The area "A" of the reaction interface increases markedly when gas is blown into the metal bath in a gas/metal system, and slag is blown into the metal bath (or metal is blown into the slag bath) in a slag/metal system; in such cases, the constant "k" also increases at the same time because of the stirring of slag or metal which accelerates the transfer of the reactants to the reaction interface. Taking a molten steel bath of volume "V" as an example, it is conceivable that the rate at which the reactants in the bath reach the reaction interface is proportional to circulating flow rate "Q" of the molten steel in the bath. The rate "Q" is related by Eq. 8 to the uniform mixing time "", which refers to the time necessary for the reactants to disperse uniformly in the bath. Time "" is related by Eq. 9 to the stirring power density "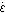", which refers to the power of stirring applied per unit weight or volume of the bath. In the refining reactions for a gas/metal system and slag/metal system, there are many cases in which Eq. 10 can be applied, even when the power for stirring is applied in different manners, such as by gas blowing, electromagnetic induction, or mechanical rotation. The reason why "n" takes the value of 0.3-0.4 has been explained for the respective stirring method in terms of transport phenomena. 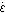However, "n" may sometimes reach 0.4-1.0 when "" increases further and metal particles disperse into the gas or slag, or gas bubbles and slag particles disperse into metal. As in the example for the rate of ore reduction by gas flowing through the charged layers of coke and ore in a BF, research on the solid phase reaction rate has also progressed to such an extent that ore reduction can be treated as the problem of a migrating boundary layer, and analysis is made by linking the ascent of the gas with the heat and mass transfer caused by the descent of lump ore and coke into the lower shaft of the BF.